This video demonstrating the Dzhanibekov effect in the microgravity of the space has intrigued me into simulating the effect myself. Dzhanibekov effect, also known as the tennis racquet theorem or the intermediate axis theorem is the phenomenon caused when rigid body with three principal axes is rotated along an axis near to its intermediate axis. When a rigid body is rotated along such an axis, the rotation is not stable as shown in the video below. Though numerical methods are used to solve the dynamics in the current post, a more analytical approach is taken in the book Classical Mechanics, Goldstein.

Lagrangian method is used to formulate the dynamics of the rigid body. The derivation is available in the Mathematica notebook in this repository. The derived dynamics is verified by the conservation of energy check and is shown below.

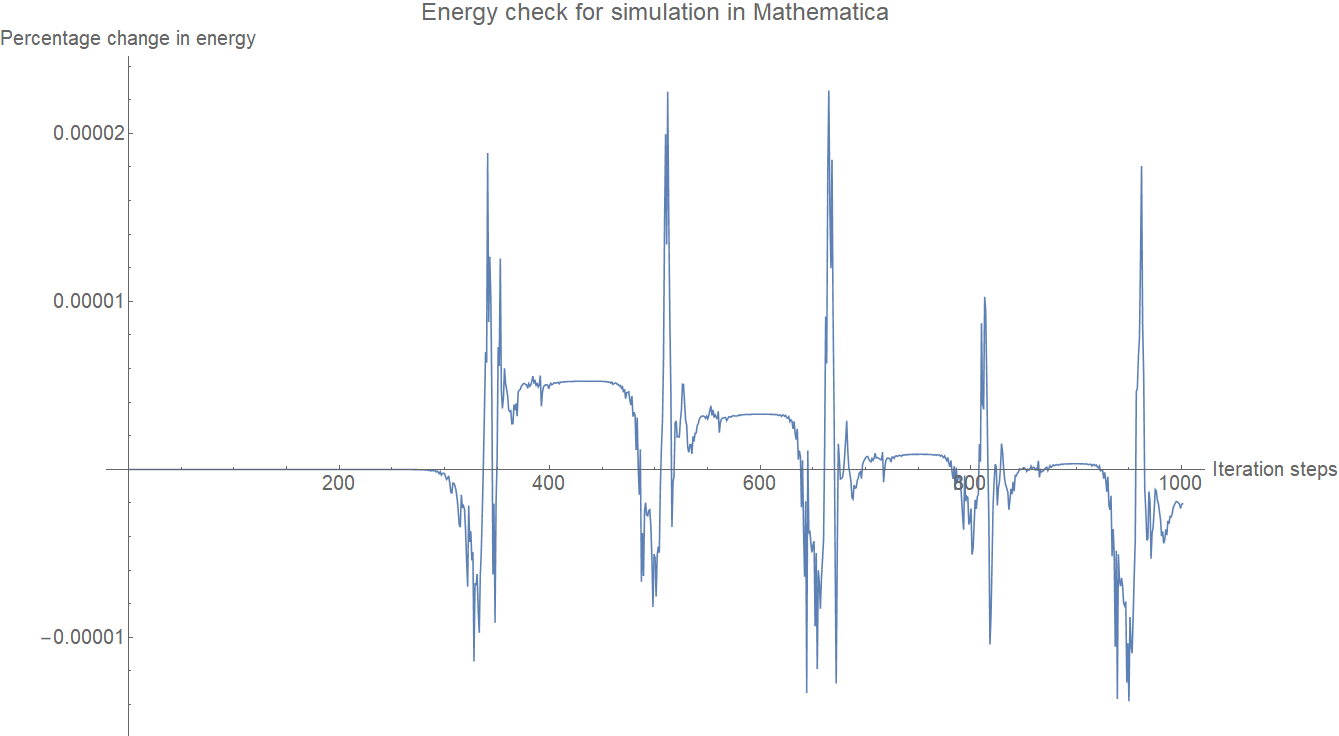
Conservation of energy check for the simulation in Mathematica

On the other hand, the same system is simulated in C++ and Fortran to compare the computation time and accuracy of the implementations. For these comparisons, none of the libraries are included, only array manipulations are used in both languages. A fixed-step fourth-order Runge-Kutta method is written to integrate the equations of motion. The implementations in both languages are available here. The result of the simulation can be seen in the video below:

Demonstration of the effect

These simulations are done on a system with the following specifications:
Processor : 4x Intel(R) Core(TM) i5-4210U CPU @ 1.70GHz
Memory : 3944MB (2797MB used)
Operating System : Ubuntu 16.04.6 LTS
Number of cores used: 1

The time and accuracy for ten simulation trails are considered for the data presented in the table. Max error is defined as the absolute maximum percentage change in the energy of the system.

Comparison between C++ and Fortran:

Language	Compilation	Execution	Max error
	time	time
C++	0.220	0.003	0.0005
Fortran	0.003	0.001	0.0020

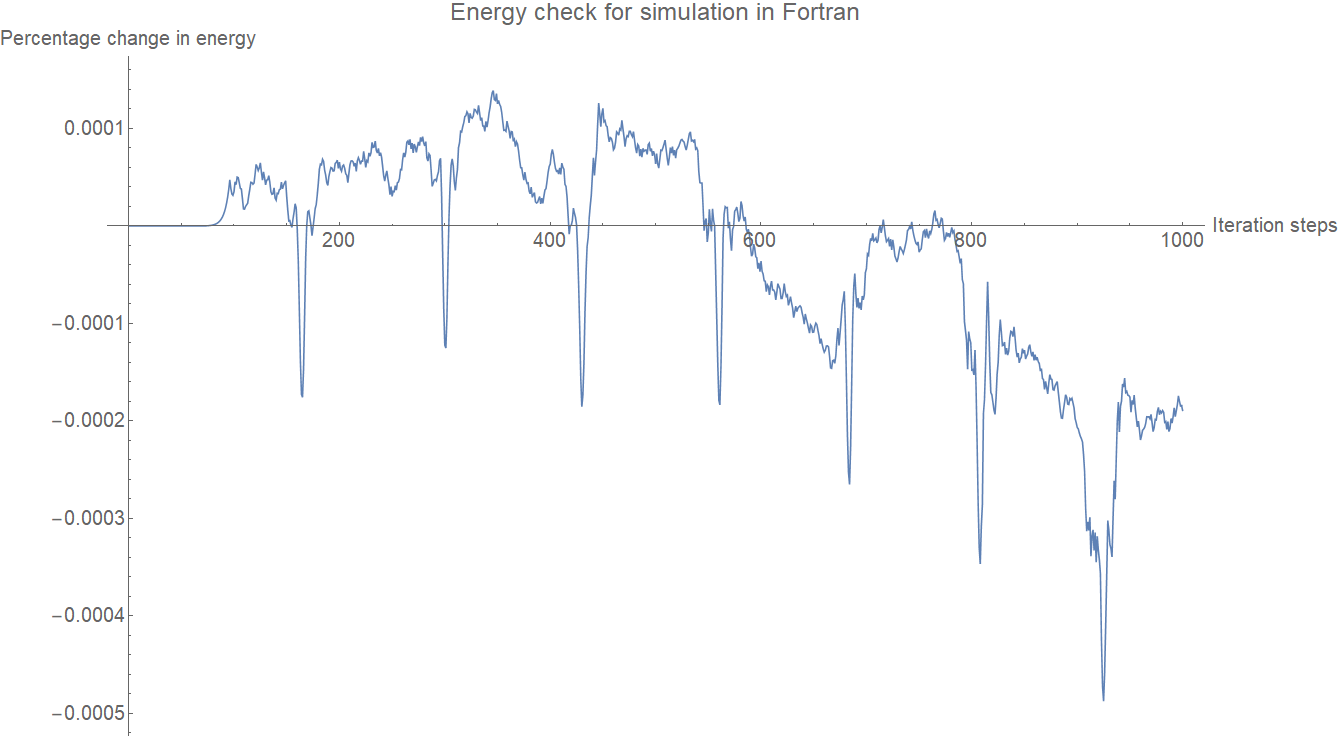
The percentage change in the energy of the system with the iteration steps for the simulation in Fortran90 is shown below.

Energy Check (F90)

The percentage change in the energy of the system with the iteration steps for the simulation in C++ is shown below.

Energy Check (C++)

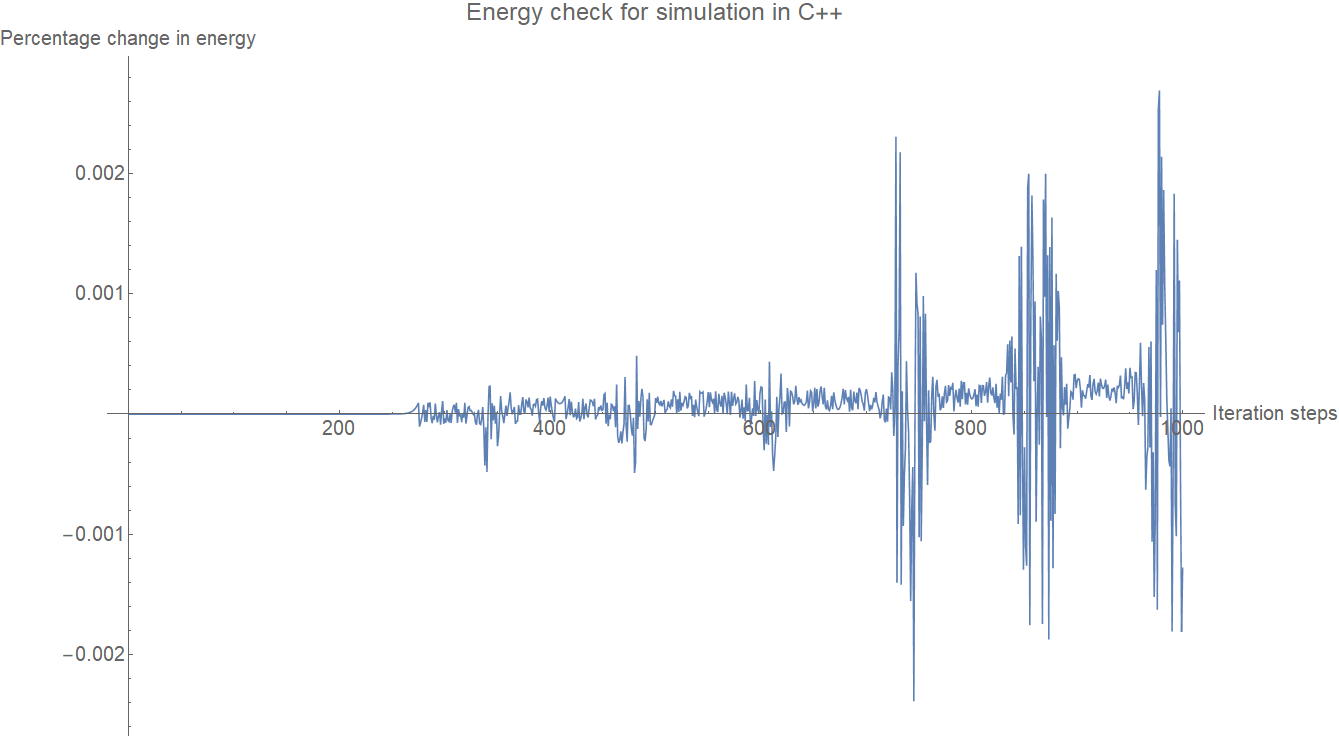
The compilers used are g++ and gfortran for codes written in C++ and F90, compiled without the use of any optimisation flags. Fortran is superior not just in execution speed but also in maintaining the accuracy in its computations. I suppose this has to do with the way floating-point operations are handled in Fortran vs C++. Although C++ is now a common tool for most of the engineers, it is always worth mentioning that when it comes to speed and accuracy Fortran beats C++ some times as in this case.

Dzhanibekov effect: Simulations in Fortran vs C++