Accessible topology optimisation

While working as a mechanical designer for the formula student electric team, we needed components which were extremely light yet functional. Components were designed based on the standards, rule book and the decided design specifications. However, I was not aware of the “right” way to reduce weight of the designed components. A popular practice used was to iteratively cut down material while ensuring the maximum stress levels to be within the tolerance. Later, I encountered a similar problem in the context of designing compliant mechanisms. In the latter case, the problem is to find a mechanism allowing maximum transfer of the input work via self-compliance. Both the scenarios point towards the concept of topology optimisation though their formulations are quite different.

Topology Optimisation:

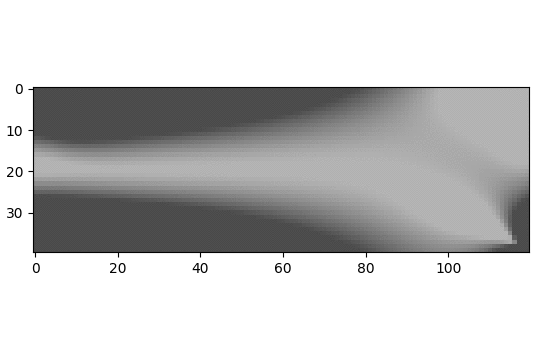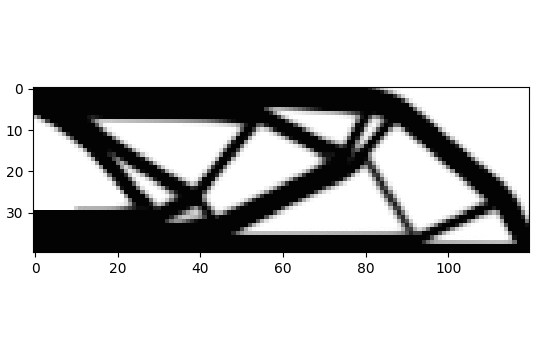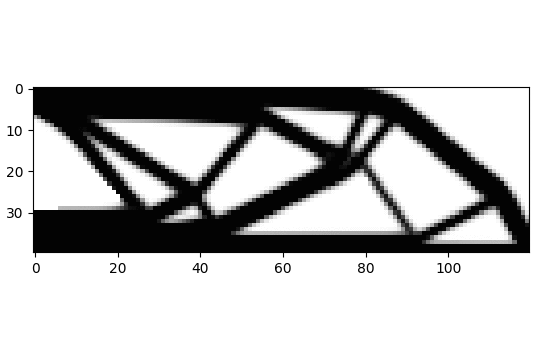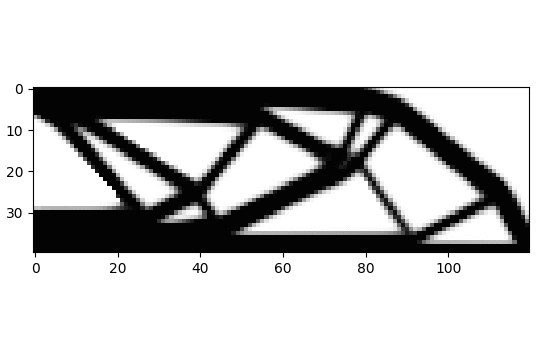
This deals with the problem of how the material needs to be distributed to achieve maximum stiffness. Topology optimisation formally poses this problem as minimising the compliance of the structure subject to the constraint on the fraction of volume required. The Fig. 1 is an example showing the progression of the optimisation problem. It deals with the example of a bridge modeled as a beam simply supported on both ends. Symmetry simplifies the problem by allowing us to model only one half of the structure. The final structure is shown in Fig. 2. You can find all about the formulation ad implementation from [1], [2] and [3].

Implementation:

The current C++ implementation was inspired from [1] which is a modified version of the famous 99 line Matlab code originally published with [2]. The current code uses the Eigen library and can be used as an example to simulate simple problems. The following are the todos for the future versions.

1. Serial implementation seriously limits the scale of problems that can be solved and parallel computation should be used wherever possible. Maximum problem size solved on my PC (Ubuntu 14.04, 4 GB RAM, Intel i5@1.7GHz) is 120x40.
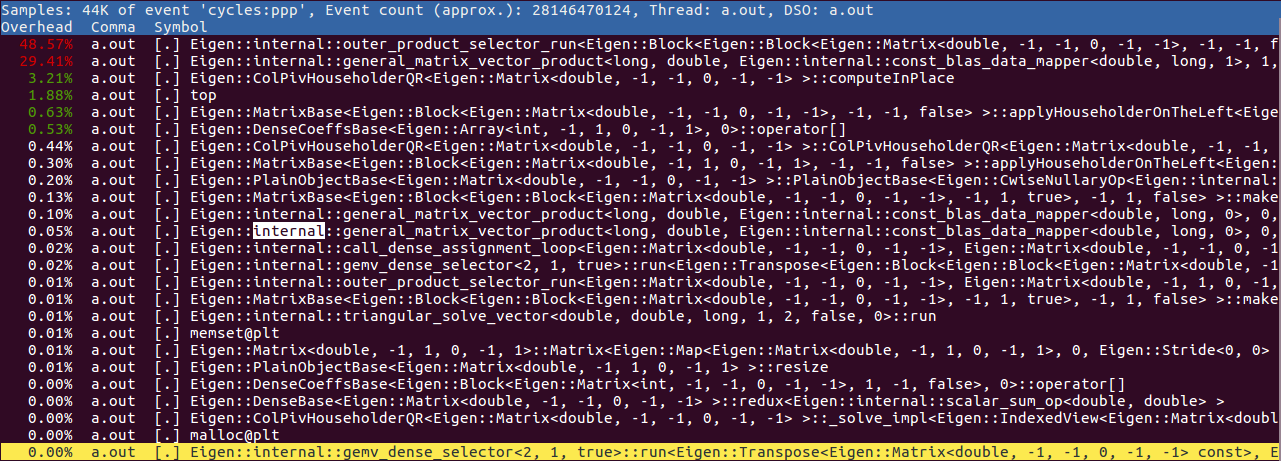
2. Profiler data shown in Fig. 3 indicates that the bottleneck as the matrix-matrix multiplications, which can be reduced significantly by using the sparse matrix implementation to represent the large matrices. Further, Eigens built-in parallelisation can be used for large matrices. Since, I did not have the required memory on my PC I couldnt solve high resolution problems.
3. Visualisation in the current code is a dirty implementation using python called at each iteration using a bash file. I had to resolve to this method after one whole night of futile attempts to plot directly from the C++ function.
   

All the required codes are available in the project GitHub repository.

References:

1. Andreassen, Erik, et al. “Efficient topology optimization in MATLAB using 88 lines of code.” Structural and Multidisciplinary Optimization 43.1 (2011): 1-16.
2. Sigmund, Ole. “A 99 line topology optimization code written in Matlab.” Structural and multidisciplinary optimization 21.2 (2001): 120-127.
3. Sigmund, Ole. “Morphology-based black and white filters for topology optimization.” Structural and Multidisciplinary Optimization 33.4-5 (2007): 401-424.