The Rising Camel Problem: Trajectory optimisation of parallel manipulators

In the robots quadruple stance phase, all the four legs of the quadruped are touching the floor, and the point of contacts of the legs with the ground does not change with time. We assume that there is sufficient friction to prevent the legs from slipping during motion. In such a condition the robot can be modelled as a parallel manipulator for analysis. The model of the robot being considered is as in [2] and is reproduced below.

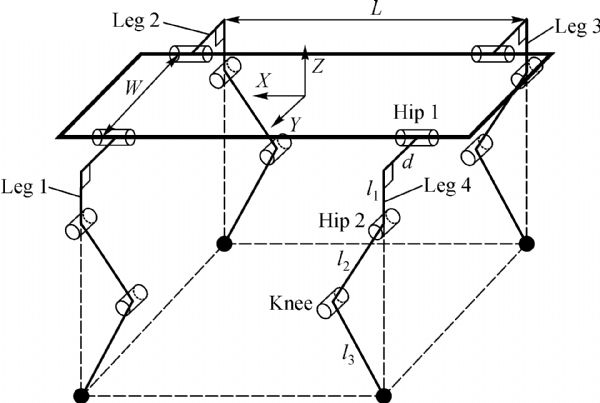
The inverse kinematic analysis is performed and is used to determine the pose of the robot as its eyes (Imaginary. Assumed to be on the midpoint of the front side of the body) track a circle. The result is as shown below.

Since the rising motion of the robot from sitting to a standing pose, is symmetric about its median plane, we consider only one half of the body.

Assumptions involved:

1. The solutions of the joint angle trajectories were approximated using fourth order polynomials.
2. The integration over the entire interval was approximated using Gaussian Quadratures instead of performing the actual integration over the whole period of motion owing to complicated dynamics of the parallel manipulator.

The above assumptions help to solve the problem in a practical amount of time. The problem was solved under various parametric conditions to investigate the characteristics of the obtained controllers. The following section contains a discussion on all the cases and the corresponding results. [1] mentions the problem of two serial manipulators cooperating in lifting a workpiece together as the rising camel problem. But here we see it from a different perspective and are modelling a camels body itself to see the motion generated by the optimal controller.

Simple shooting:

As a first step, we tried solving the full control problem. The dynamics turned out to be too complicated to integrate for the whole period. So we start by ignoring the effects of gravity and use a feedback-linearised model. The solution to this problem is shown in the video below. It is seen that the presence of the third actuator in an asymmetric position did not affect the solution at all. The entire motion was symmetric, meaning that the model is decoupled, as the complex coupling terms are missing.

Without Gravity:

To solve the full problem instead of searching the full space we’ll instead start approximating the trajectory with at least a polynomial of fourth order(as we know the end configurations of each state to be controlled) and use a Gaussian integration to integrate within the given time interval.

Experiment:

The same construction of the manipulator, as shown above, was considered and the problem of rising to a final state is performed without considering the effects of the gravity first. The tests were performed parametrically by changing the number of Gauss Quadrature sampling points. The following are the results obtained. The results obtained were different from the one obtained from decoupling the problem. This confirms the solution obtained by using a simple feedback linearised model is incomplete. This decouples the problem loosing valuable trajectories which might exploit the coupled effects in the dynamics.

With Gravity:

This deals with the raising camel problem in its full glory. This problem is the same as the above but considering the effects of gravity in this case. The test is performed with changing Gauss Quadrature interpolation points. The result for 5 points is as shown in the video below. One can see a striking similarity between the optimal solution between this and a camel rising. Though both of these models differ in terms of construction, i.e. the number of degrees of freedom and the number of links (bones involved) and the type of actuation itself, the solution can be seen very relevant.

Unrealistic Mass Experiment:

The body link is given a very high mass to see if it could come up with a control strategy to reach the final pose. The following is the result. The result gives us some interesting insights into how the task was solved.

The inspiration for this experiment is [1], speaking about power lifting of a load more than the prescribed value by a PUMA robot. We wanted to see if we can observe such joint trajectories to lift a very high body mass.

Interpretation: Initially, instead of lifting the link to the final state it lets gravity do the job for it. While transitioning from moving downward to upward, it makes sure that the left part of the linkages are aligned such that the load is entirely taken by the ground joint so that there is no additional effort by the motors in lifting it. Before rising itself up, it moves almost in a straight line path, which implies that there is no change in its potential energy throughout that motion.

The manipulator was enforced to reach a final end state, so the final total energy is the potential energy of all the links only. Since the net energy is the energy being pumped by the motors, the interest of the motors is to take the body link to the top and hence the energy pumped into the system shouldn’t be wasted as potential energy of the system. So the manipulator tries to maintain the body in the horizontal position, i.e. no energy is used in changing the potential energy of the links, but all the energy pumped in is the kinetic energy of the high massed link. Thus once the transmission angle is optimal, the other actuator directly goes to full actuation pushing the link to the final state. This explains that horizontal path.

The major difference between the rising camel problem talked about in [1] vs here is that the contact force between the serial manipulator and the workpiece might be limited, but these ideal passive joints allow theoretically infinite forces. Also, it is clearly observed that through a large part of the trajectory the manipulator prefers a singular pose, at which some of the load of the link is taken by the structure itself rather than the actuators working against them and spending energy.

Acknowledgments:

The project was done in collaboration with my colleague R. Gautham for the course “Design, Analysis and Control of Parallel Manipulators”, instructor, Prof. Sandipan Bandyopadhyay. For further information, please find the complete project report below.

Rising Camel Project Report

References:

1. J. E. Bobrow et. al., “Optimal Robot Motions for Physical Criteria”, Journ. of Robotic Systems, 2001
2. Jingjun YU, et.al., ”Motion capability analysis of a quadruped robot as a parallel manipulator”, Front. Mech. Eng., 2014