Kalman Filter Implementation

This project is an implementation of an Extended Kalman Filter on the data given in [1]. Kalman Filter is also called Linear Quadratic Estimator(LQE). Given a non-linear model of a system, the error covariance of the sensors and the model and the Jacobian, the code implements an EKF for the given data to give better estimates of the corresponding data.

In implementing the extended Kalman Filter the there are two parts, one, the actual Kalman Filter step and the other is to find the Jacobian of the system in parallel, to get instantaneous linearised system coefficients. These linearised coefficients which are in the continuous time domain need to be changed to discrete time to plug into the formulation.

For a set of assumed initial conditions, the following figure shows the working of the filter. Filtered estimates having lower noise are as shown below.

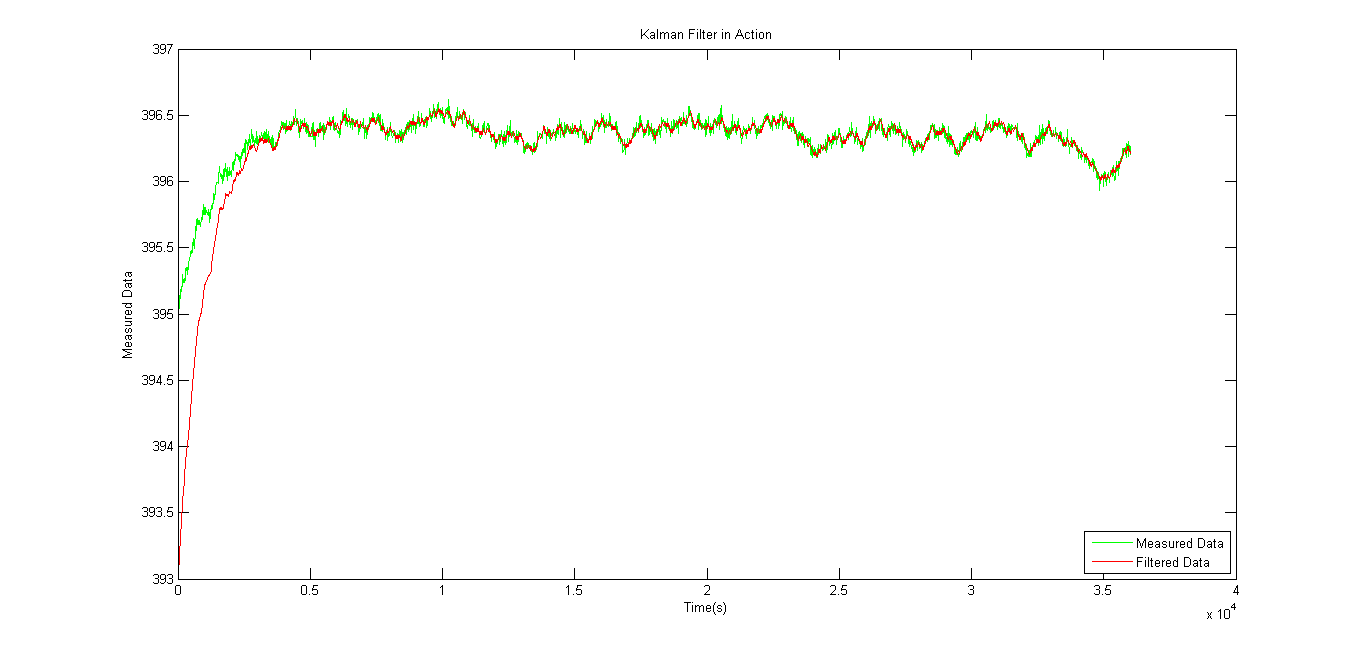
The filter converges, irrespective of the initial guess. The convergence of the filter from a different initial value is as shown below.

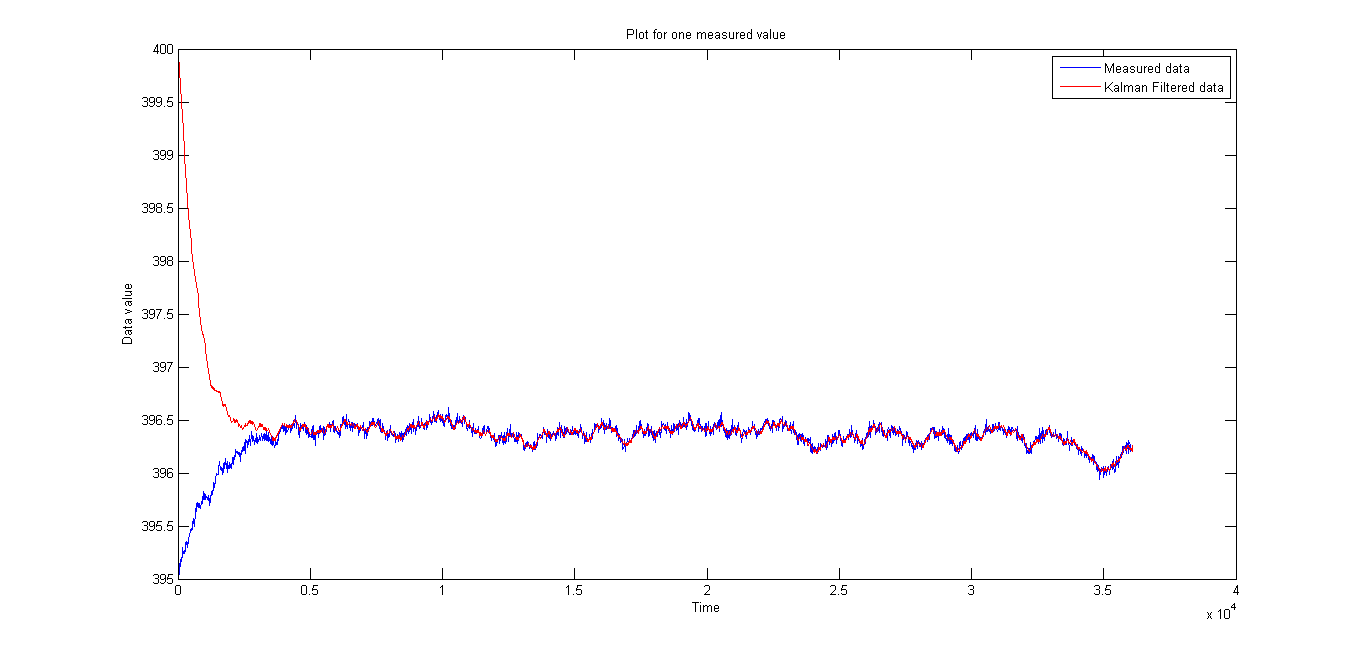
References:

[1] Balchen, Jens G., Dag Ljungquist, and Stig Strand. “State—space predictive control.” Chemical Engineering Science 47.4 (1992): 787-807.